| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- php
- vagrant
- 에러해결
- 보안
- MySQL
- centOS7
- linux #centos
- 개인공부
- laravel
- 네이버싫어
- php artisan
- 기타정리
- 작업물
- 일상
- 메모
- ratchet
- 복습 #회사
- 카카오가고싶다
- centOS
- php-fpm
- error
- 작업물 #영상편집 #서브컬쳐
- Backend
- AWS
- 시벌이슈
- 키워드
- 코딩테스트
- jquery
- 키워드 정리
- NGINX
- Today
- Total
개발을 간바루Joy 하게
#4 반복문 vs 순환문 본문
컴퓨터 프로그래밍을 하다 보면 무언가를 되풀이하는 경우가 많다.
대표적으로 for문이나 while문 등의 반복문이 있다.
for 문은 변수를 이용해서 반복 횟수를 제어하며, 그 만큼 반복하는 것이고 while 문의 경우 조건문에 의하여 반복하는 것이다.
하지만, 반복문을 사용하게 되면 복잡해지는 문제들이 존재한다. 이런 경우에 순환을 이용하여 코드를 짜면 좋다.
반복과 순환에 대해 알아보고 비교해보자.
반복은 반복문을 이용하여 되풀이하는 구조이다. 수행 속도가 빠르다는 장점이 있는 대신, 코드 작성이 순환문에 비해 어렵다.
다음은 팩토리얼 함수를 반복문으로 짠 구조이다.

다음 알고리즘을 빅오 표기법으로 표현해보면, O(n)의 시간 복잡도를 가지게 된다. for문을 통해 곱셈을 n번 수행하기 때문이다. (T(n)=n)
순환은 주어진 문제를 해결하기 위해 자기 자신을 다시 호출하여 작업을 수행하는 방식이다. 순환적인 문제는 순환문을 사용하는 것이 좋다. 코드 작성이 반복문에 비해 쉽기 때문이다.
그 예로 팩토리얼 함수, 이진 트리 알고리즘, 이진 탐색, 하노이 탑 등이 있다. 하지만, 함수를 스택에 저장해 호출하는 방법이므로 시스템에 무리가 간다는 단점이 있다.
다음은 팩토리얼 함수를 순환문으로 짜는 구조이다.

순환문은 순환을 멈추는 부분과 순환 호출을 하는 부분으로 나뉘어 있다.
다음 함수를 보면, if 절에서 순환을 멈추고 else 절에서 순환 호출을 하고 있다.
만약, 순환을 멈추는 부분이 없이 계속 순환 호출을 한다면 무한히 순환 호출을 하게 되어 오버플로우를 발생시킨다.
따라서 순환문에는 반드시 순환을 멈추는 부분이 존재해야 한다.
다시 else 절을 보면, 문제의 일부를 해결하고 남은 부분은 다시 함수를 호출하고 있다.
순환은 분할정복법(문제를 나눠서 해결하는 방법)을 사용하는 구조임을 알 수 있다.
다음을 빅오 표기법으로 표현해보면, 반복문과 같이 O(n)의 시간 복잡도를 가진다. 한번 순환 호출될 때마다 곱셈 연산을 한 번 수행하기 때문이다. (T(n)=n)
순환적인 문제이지만, 순환문보다 반복문이 좋은 경우가 존재한다.
피보나치 수열이 대표적인 예시인데, 피보나치 수열은 앞의 두 수를 더해 다음 수를 만든다.
제 0항이 0, 제 1항이 1인 수열이 시작된다고 가정하면, 0,1,1,2,3,5,8,... 이런 식으로 수열이 생기는 방식이다.
이것을 순환문으로 표현하면 다음과 같다.
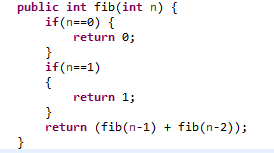
여기서 n은 제 n항을 의미한다.
이 코드의 문제점은 계산했던 값을 다시 구하여 다시 계산하기 때문에 n이 커질수록 함수 호출도 매우 늘어난다.
만약 n=6 이라면, fib(3)만을 세 번 호출하게 되며, fib() 전체 수의 경우 25번이나 호출된다.
이런 경우가 순환적인 문제지만, 반복문이 더 좋은 경우가 된다.
이 알고리즘을 빅오 표기법으로 표현하면, T(n)=T(n-1)+T(n-2)+1 이고 이것을 풀면 O(2^n)의 시간 복잡도를 가지게 된다.
이번엔 피보나치 수열을 반복문으로 짜보자.

순환문과 달리 중복 항 계산이 없어 더욱 효율적이다.
이를 빅오 표기법으로 표현하면, T(n)=n+1 이므로 O(n)의 시간 복잡도를 가지게 된다.
'프로그래밍 > 자료구조, 알고리즘' 카테고리의 다른 글
| #3 알고리즘 성능 분석: 시간 복잡도 분석, 빅오(Big-O) 표기법 (0) | 2020.02.04 |
|---|---|
| #2 자료형이란? (0) | 2020.02.03 |
| #1 자료구조와 알고리즘이란? (0) | 2020.02.03 |

